Bad takes #2. Evolution by “mutation pressure”
Unfamiliar ideas are often mis-identified and mis-characterized. It takes time for a new idea to be sufficiently familiar that it can be debated meaningfully. We look forward to those more meaningful debates. Until then, fending off bad takes is the order of the day! See the Bad Takes Index.
In his equally entertaining and obnoxious piece “The frailty of adaptive hypotheses for the origins of organismal complexity,” Lynch (2007) writes
The notion that mutation pressure can be a driving force in evolution is not new (6, 24–31)
citing works of Darwin, Morgan, Dover, Nei, Cavalier-Smith, and Stoltzfus and Yampolsky.
What does it mean to invoke evolutionary change due to a driving force of mutation pressure? This language suggests a process of population transformation by the mutational conversion of individuals, in contrast to population transformation by reproductive replacement.
That is, in a simplified world of discretely inherited types, we can imagine two general ways to transform a reproducing population from mainly type A to mainly type B. One mode is for an initially rare type B to take over the A population, over many generations, by the cumulative effects of differential reproduction, either biased (selection) or unbiased (drift). Individuals of type B over-produce, while A individuals die out, so that A individuals are replaced by unrelated B individuals. This is usually how we think about the transformation of populations: reproductive replacement. Selection and drift are often listed as the two main causes of evolution, and they act by reproductive replacement.
A second possible mode of change is for a population of predominantly A individuals to change by many separate events of A-to-B conversion (either individual conversion, or the cross-generational conversion of a lineage from parent to offspring). In this case, A individuals are lost, not by death, but by conversion, and likewise, B individuals are over-produced, not by the excess reproduction of B parents, but by conversion from A individuals. This process might take a single generation or many generations, depending on the rate of conversion (see image for a simulation).
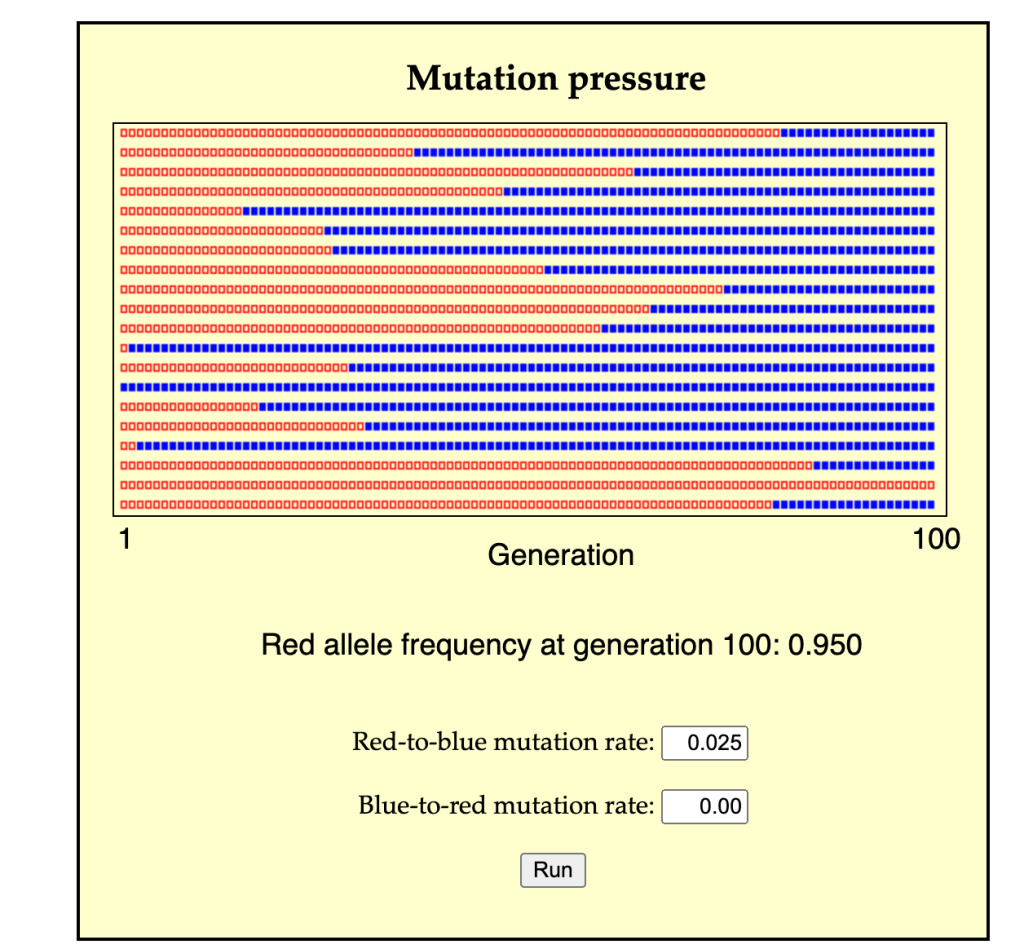
In a more complex scenario, there are other possibilities. For instance, given diploid inheritance we could consider a process of biased gene conversion by which A1A2 genotypes are converted into A2A2. Suppose that A2 is recessive so that A1A1 and A1A2 have phenotype P1, and A2A2 has P2. In this scenario, biased gene conversion can transform a predominantly P1 population into a P2 population. Dover’s ideas about molecular drive combine effects of conversion and replacement.
One of the minor theories in Darwin’s Origin of Species is the mass transformation of individuals by direct effects of the environment. This idea was not unique to Darwin, but simply reflected 19th-century thinking by which heredity is (in effect) mediated by responsive memory-fluids that circulate in the body: after collecting bodily experiences, the memory-fluids gather in the gametes, and during reproduction, they blend, passing on a blended version of inheritance plus experience. Given this view, it was natural to suppose that, when animals or plants encounter a new environment, this results in a hereditary transformation by the cumulative effect of many environment-induced conversions.
The literature of the pre-Synthesis period includes some (typically ambiguous) references to population transformation by mutational conversion, e.g., Shull (1936) writes
If a given mutation were to happen often enough, and nothing opposed its survival, it could easily spread through the entire species, replacing all the other genes at the same locus.
Evolution by mutation pressure according to Haldane and Fisher
In the broader context of evolutionary theorizing, the mutation pressure theory appears most prominently as a strawman rejected by Haldane (1927, 1932) and Fisher (1930). That is, Haldane and Fisher did not advocate the notion of evolution by mutation pressure, but presented an unworkable theory as a way to reject the idea, popular among critics of neo-Darwinism, that evolutionary tendencies may reflect internal variational tendencies. In reality, the early geneticists typically argued, not for mutational transformation of populations, but for a two-step process of “mutation proposes, selection disposes” (decides); and the idea of orthogenesis was typically an appeal to what we might call “constraints” today. That is, the mutation pressure theory began as a dubious take on internalist thinking.
Regardless, Haldane and Fisher worked out the implications of evolution by mutation pressure, finding it unlikely on the grounds that, because mutation rates are small, mutation is a weak pressure on allele frequencies, easily overcome by opposing selection. Haldane concluded that this pressure would not be important except in the case of neutral characters or abnormally high mutation rates.

To understand what Haldane is doing, one must bear in mind that, in the neo-Darwinian tradition, selection is the model of an evolutionary cause: other factors or processes are considered to be causal only to the extent that they look like selection. What selection does is to shift frequencies (and ultimately drive alleles to fixation), so Darwin’s modern followers define evolution as shifting frequencies and they define causal forces as pressures that might cause fixation. In effect, Haldane equates the importance of mutation with the potential for mutation pressure to drive allele frequencies. In this way of thinking, if mutation-biased evolution is happening, this is because mutation is driving alleles to high frequency against the opposing pressure of selection, which leads to Haldane’s conclusion that either (1) the mutation rate has to be abnormally high, or (2) selection has to be practically absent (i.e., neutrality). Fisher’s (1930) reasoning was similar. From the observed smallness of mutation rates, he drew a sweeping conclusion to the effect that internalist theories are incompatible with population genetics.
Provine (1978) identifies this argument (against evolution by mutation pressure) as one of the key contributions of theoretical population genetics to the Modern Synthesis, because it gave Darwin’s followers a seemingly rigorous basis to reject internalist theories (establishing the core Synthesis principle of There Is No Alternative). The argument was cited repeatedly by the architects of the Modern Synthesis (for examples, see Stoltzfus, 2017), and continues to be cited, e.g., Gould (2002) cites Fisher’s version of the argument and concludes that
Since orthogenesis can only operate when mutation pressure becomes high enough to act as an agent of evolutionary change, empirical data on low mutation rates sound the death-knell of internalism. (p. 510)
Subsequent work has partially undermined the narrow implications of the Haldane-Fisher argument, and completely undermined its broader application as a cudgel against internalism. Mutation pressure is almost never a reasonable cause of population transformation, because it would happen so slowly and take so long that other factors such as drift would intervene, as argued by Kimura (1980). The case studied by Masel and Maughan (2007) is a rare example in which evolution by mutation pressure is reasonable: the authors estimate an aggregate mutation rate of 0.003 for loss of a trait (sporulation) dependent on many loci, concluding that complex traits can be lost in a reasonable period of time due primarily to mutational degradation.
Thus, in spite of what one would conclude from Haldane (1927), patterns of mutation bias in evolution generally do not indicate evolution by mutation pressure via high mutation rates, or via neutral characters. Mutation-biased neutral evolution happens, not because mutation pressure is driving alleles to fixation in a biased way (instead, drift is the cause of fixation), but due to a bias in the origination process. And of course, Yampolsky and Stoltzfus (2001) showed that, when there is a bias in the introduction process, this can impose a bias on the course of evolutionary change even when fixations are selective, i.e., there is no requirement for neutral evolution.
In summary, the classic theory of evolution by mutation pressure is not much use in understanding evolution, and is mainly of historical interest for its role in an influential fallacy: generations of evolutionary thinkers believed wrongly that the mutation pressure theory proves mathematically that internalist theories are incompatible with population genetics.
Other theories
Now, with this background, we may return to Lynch’s bad take, associating various authors with mutation pressure as a driving force. Of the authors cited — Darwin, Morgan, Dover, Nei, Cavalier-Smith and my colleagues and I — none of them directly propose a theory of evolution by mutation pressure. However, the ideas of Darwin and Dover depict a process reliant on mass conversion: in Dover’s case, population transformation takes place by a dual process of conversion (gene conversion or sub-genomic replication) and reproductive replacement, and in Darwin’s case, it takes place by direct inherited effects of the environment.
Nei refers to “mutation-driven” evolution (the title of his 2013 book), but this is not a reference to mutation driving alleles to fixation. Nei’s usage of “drive” is descriptive or explanatory: evolution is mutation-driven to the extent that our understanding of important aspects of the course of evolution relies on knowing which mutations happen at what times. The same meaning is used in “Mutation-Driven Parallel Evolution During Viral Adaptation” (Sackman, et al. 2017). For an explanation of this meaning of “drive,” see Bad Take #4.
Likewise, the work from my colleagues and me is not about evolution by mutation pressure. From the very beginning, we have (1) followed Provine (1978) in noting the historical importance of the Haldane-Fisher argument against evolution by mutation pressure, and (2) promoted a theory for the effects of biases in the introduction process, obviously a different theory because it contradicts the implications of the mutation pressure theory.
So, what on earth does Lynch mean when he refers to evolution driven by mutation pressure? This is unclear. The model that Lynch (2007) presents immediately after the quoted statement is not a model of evolution by mutation pressure in the classic sense of Haldane and Fisher and IMHO does not correspond to what any of the cited authors are trying to say.
To understand what the model tells us, we must analyze it in detail, in comparison to the classic mutation-selection balance (also co-developed by Haldane and Fisher). The forces of population genetics are conceptualized like the laws of statistical physics, as mass-action pressures on allele frequencies due to the aggregate effect of countless individual events. In the case of mutation, countless individual events of mutational conversion from allele A1 to allele A2 result in a force or pressure of mutation shifting quantities of A1 to A2. Because there are innumerable independent events, each with an infinitesimal effect, we can represent the aggregate effect with a continuous quantity, e.g., we can write fA2‘ = fA2 + u fA1 to indicate the increase in fA2 due to mutation at rate u from allele A1, and we can write fA1‘ = (1 – u) fA1 to represent the corresponding reduction in the frequency of allele A1 due to mutation to allele A2.
In the classic conception of the mutation-selection balance, if A1 is favored over A2 by a selection coefficient s, then reproductive replacement by selection represents a pressure of magnitude s increasing fA1 and decreasing fA2, whereas mutation is a pressure of magnitude u with the opposite effect, acting by conversion (rather than reproductive replacement). The equilibrium frequency of A2 is roughly f = u / s, and this is typically a small number (much closer to 0 than to 1) because mutation rates are very small, e.g., a typical rate for a specific nucleotide mutation is 10-9 per generation. This is why Haldane concluded (above) that mutation would be unimportant unless selection is effectively absent (i.e., neutrality) or mutation rates are abnormally large (note how the classical mutation-selection balance of Haldane and Fisher is closely related to their argument about evolution by mutation pressure).
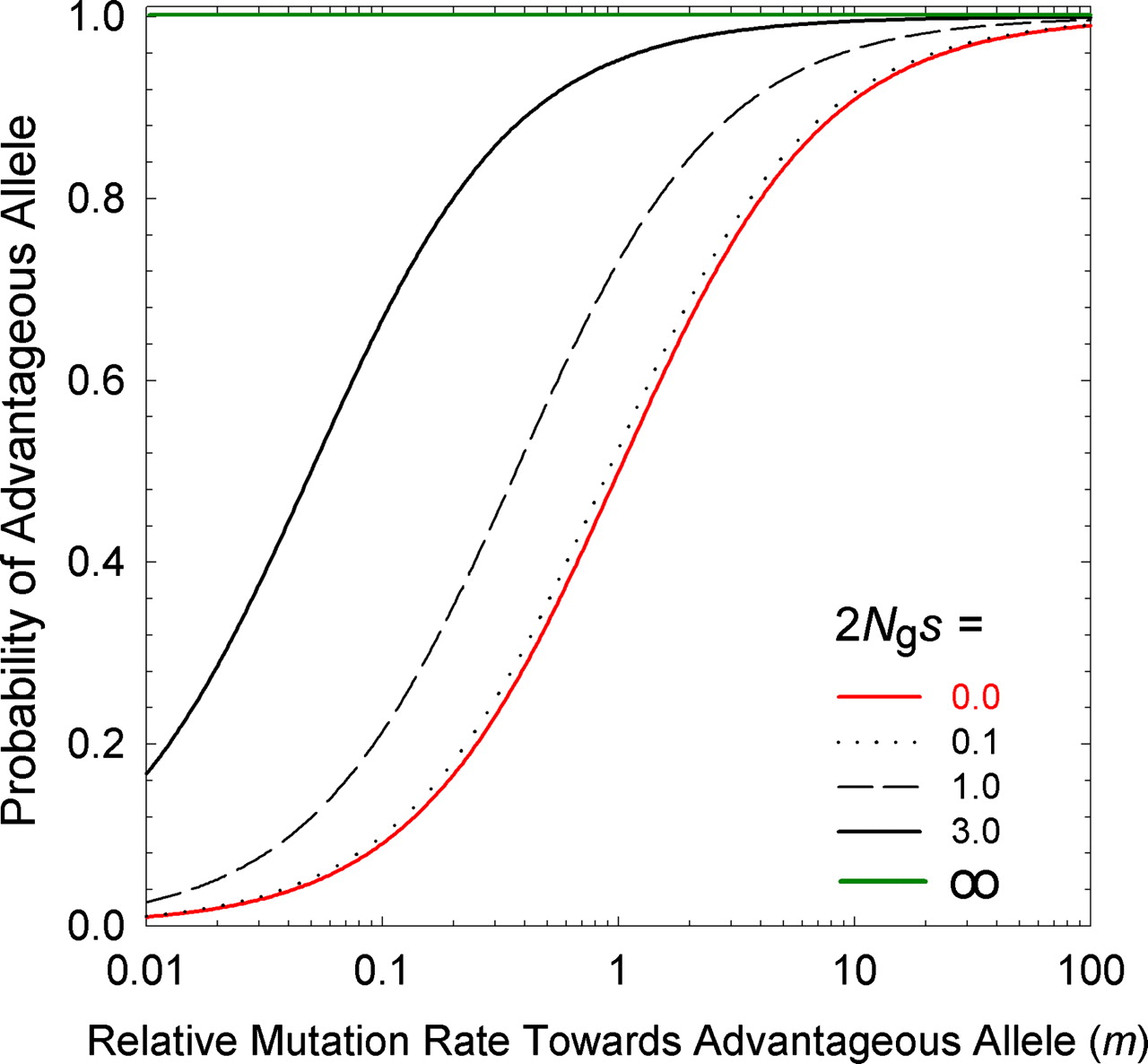
Lynch appears to reach a different solution to the same problem of the equilibrium frequency in a 2-allele system. His equation for the ratio of A1 to A2 is meS, where m is the forward-backward mutation bias favoring A1, and eS is the ratio of fixation probabilities where upper-case S = 2Ngs and lower-case s has the same meaning as above. However, this result actually does not represent the equilibrium frequency of A1 in a population of individuals, as for Haldane-Fisher: instead, it refers to the equilibrium distribution of infinitely many loci subject to an origin-fixation process, where each locus is fixed for A1 or A2, that is, meS is the expected ratio of (1) the fraction of loci fixed for A1 to (2) the fraction of loci fixed for A2.
This is easier to understand with a concrete example: the relative genomic frequency of two synonymous codons like CAT and CAC encoding histidine, where one of the codons (let’s assume CAC) is slightly more favored by selection.
The two cases, classic and Lynch, correspond to the large-population and small-population approximations for the ratio of favored to disfavored codons in Bulmer’s (1991) mutation-selection-drift model. In a large deterministic population, each histidine codon is fixed for the favored synonym (CAC), yet the disfavored codon (CAT) is maintained at low frequency in mutation-selection balance per Haldane-Fisher. In the small population, each histidine codon is fixed for either the favored codon (CAC) or the disfavored codon (CAT), and the frequency distribution of fixed states for loci is determined by the balance of two origin-fixation rates. So, in either case, if the disfavored codon is expected a fraction f of the time, then f is also the expected frequency of that codon over an infinite genomic set of histidine sites.
Thus, Lynch’s argument gives a different result because it refers to a different kind of mass-action pressure than Haldane and Fisher conceived. The relevant pressure in Lynch’s argument is the mass-action pressure due to events of origination aggregated over an infinite distribution of loci (sites). This origination pressure is not the same as classic mutation pressure, which is the mass-action pressure due to mutational conversion events aggregated over infinitely many alleles (in a population) at the same locus.
The result of this pressure (relative to a deterministic universe with only the favored codon), is to ensure that, for small values of S = 2Ngs, a substantial fraction of loci are fixed for the disfavored state; when S = 2Ngs becomes modestly large, this fraction is negligible. That is, mutation pressure, for Lynch, refers to something that ensures the predictable presence of deleterious states. By contrast, the theory of Yampolsky and Stoltzfus (2001) is about the way that biases in origination impose biases on which path, out of many possible, is taken by adaptation.
Clearly this model ensures the presence of deleterious states for small values of S, but it is not clear what justifies Lynch’s framing of this as an effect of a pressure of mutation (more precisely, a pressure of origination), rather than as an effect of random drift or of origin-fixation pressure. Mutation and fixation do not act separately in the context of the argument, and drift is profoundly important in ensuring that, in Lynch’s stochastic anti-paradise, a substantial fraction of everything is in a sub-optimal state. In a world that has deterministic selection, the favored codon always wins (and the disfavored one is never fixed by chance), even in small populations, and this will be true regardless of what we assume about mutation. Metaphorically, mutation is just knocking at the door, offering bad choices: drift has to open the door and let them in. On this basis, Lynch ought to point the finger at drift (not mutation) as the reason for non-optimality.
In fact, this is all utterly misleading when taken in context. After telling the reader that the idea of evolution by mutation pressure is not new, Lynch continues as follows
The notion that mutation pressure can be a driving force in evolution is not new (6, 24–31), and the conditions that must be fulfilled if mutation is to alter the direction of evolution relative to adaptive expectations are readily derived.
This is a sweeping claim about mutation and directionality! Yet, what follows is not a general model of effects of mutation on the direction of evolutionary change, but Bulmer’s model featuring fixations of deleterious alleles! That is, Lynch refers generally to mutational effects altering the “direction” of evolution, yet apparently, given his Manichean worldview, “direction” is just a matter of down vs up in fitness. And we just established that drift, not mutation, is the cause of deleterious fixations, which will happen even if there is no mutation bias (e.g., the disfavored codon will sometimes be fixed, even without any mutation bias). In the end, Lynch has presented correct mathematical results, but framed these results in an incorrect way that can only lead to confusion.
Accordingly, Svensson (here or here) has repeatedly claimed, citing Lynch’s paper, that an effect of mutation bias on adaptation would require “drift in small populations.” This error arises from a literal reading of Lynch, who (1) conflates diverse ideas (including ours) under the heading of evolution by mutation pressure, and then (2) makes a sweeping reference to mutational effects on “direction.” However, as explained, the effect requiring small populations in Lynch’s model is the fixation of a slightly deleterious allele by drift in small populations, whereas arguments about mutation-biased adaptation do not involve fixations of deleterious alleles at all, e.g., the behavior of the Yampolsky-Stoltzfus model does not rely in any sense on the fixation of deleterious alleles by drift.
What is the cause of so much misapprehension? The molecular revolution induced profound changes in thinking that have not been properly processed. Instead, we have attempted to squeeze a new understanding into the same old vocabulary— using old words for new concepts. In some cases, the result is verbal violence, as in the way that “Darwinian adaptation” is now used for the lucky mutant view previously known as a non-Darwinian theory of pre-adaptation. Familiar words are now overloaded with different concepts, and we have not paid attention to the problems caused by this overloading. Evolution by mutation pressure, in the classic Haldane-Fisher sense, means something different than what Lynch’s model means, which is something different than what the Yampolsky-Stoltzfus model means. The forces theory is inadequate, and leads scientists to incorrect conclusions, e.g., the assumption that mutation-biased evolution requires neutrality, which is pervasive in the literature.
The path toward greater clarity depends on making distinctions, e.g., distinguishing the introduction (origination) process from classical mutation pressure (across infinitely many copies of an allele in a population) and from origin pressure (across infinitely many loci). The reason to distinguish these, again, is that they behave differently, so that the rules for reasoning about one kind of causal process are different from the rules for reasoning about another.
Likewise, one must bear in mind that biological processes are not the same as the operators in models or mathematical formalisms, which capture only some of implications of biological processes for evolution. The classic conception of forces in population genetics includes a thing with the label “mutation” (and another thing with the label “selection”), but this thing does not have all the same implications as the biological process with the label “mutation.”
Sources that fail to make such distinctions will mislead readers with the impression that every reference to mutation is a reference to exactly the same evolutionary theory, when this clearly is not the case.
References
- Fisher RA. 1930. The Genetical Theory of Natural Selection. London: Oxford University Press.
- Gould SJ. 2002. The Structure of Evolutionary Theory. Cambridge, Massachusetts: Harvard University Press.
- Haldane JBS. 1927. A mathematical theory of natural and artificial selection. V. Selection and mutation. Proc. Cam. Phil. Soc. 26:220-230.
- Haldane JBS. 1932. The Causes of Evolution. New York: Longmans, Green and Co.
- Haldane JBS. 1933. The part played by recurrent mutation in evolution. Am. Nat. 67:5-19.
- Kimura M. 1980. Average time until fixation of a mutant allele in a finite population under continued mutation pressure: Studies by analytical, numerical, and pseudo-sampling methods. Proc Natl Acad Sci U S A 77:522-526.
- Lynch M. 2007. The frailty of adaptive hypotheses for the origins of organismal complexity. Proc Natl Acad Sci U S A 104 Suppl 1:8597-8604.
- Provine WB. 1978. The role of mathematical population geneticists in the evolutionary synthesis of the 1930s and 1940s. Stud Hist Biol. 2:167-192.
- Shull AF. 1936. Evolution. New York: McGraw-Hill.
- Stoltzfus A. 2006. Mutationism and the Dual Causation of Evolutionary Change. Evol Dev 8:304-317.
- Yampolsky LY, Stoltzfus A. 2001. Bias in the introduction of variation as an orienting factor in evolution. Evol Dev 3:73-83.
Notes
Biased gene conversion is a newly recognized population-genetic force, non-identical with mutation, selection, or recombination. BGC is a conversion mechanism, not a replacement mechanism, but the formula for BGC is A1 + A2 –> A2 + A2, whereas the mutation formula is A1 –> A2. Similarly, the crossing-over formula is A1B1 + A2B2 –> A1B2 + A2B1. Thus, although the molecular operation of gene conversion is associated with cross-overs and with the machinery for recombination, the genetic operation of BGC is not the same thing as recombination.